电子结构分析

发表于 | 分类于 | 本文总阅读数 次

分子轨道理论

原子轨道和分子轨道都是波函数。分子轨道是原子轨道交叠的结果，也就是原子轨道波函数相互干涉的结果。

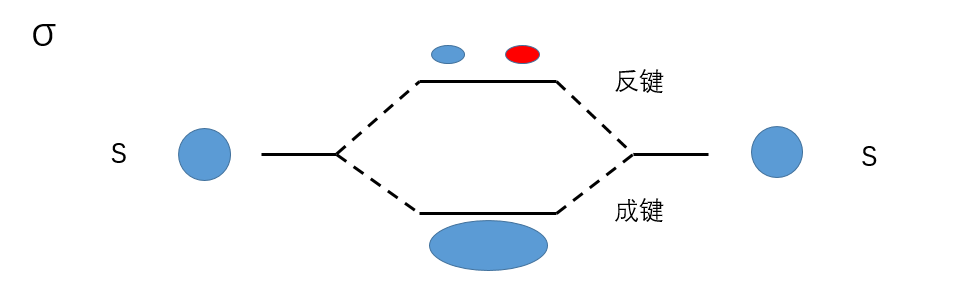
对于成键轨道σ1s，是两个原子轨道1sa和1sb相长干涉的结果：

(σ1s)2=(1sa+1sb)2=1sa2+1sb2+21sa1sb(\sigma_{1s})^{2} = (1_{sa}+1_{sb})^2=1_{sa}^2+1_{sb}^2 + 21_{sa}1_{sb}

可以发现相长干涉导致增加了21sa1sb21_{sa}1_{sb}项，导致原子间概率密度增加，能量降低，成键轨道能量降低。

对于反键轨道σ1s*，是两个原子轨道1sa和1sb相消干涉的结果：

(σ1s∗)2=(1sa−1sb)2=1sa2+1sb2−21sa1sb(\sigma_{1s}^*)^{2} = (1_{sa}-1_{sb})^2=1_{sa}^2+1_{sb}^2 - 21_{sa}1_{sb}

可以发现相消干涉导致减少了21sa1sb21_{sa}1_{sb}项，导致原子间概率密度减少，能量增加，成键轨道能量增加。

原子轨道分布图描述的是解薛定谔方程得到的波函数ψ的值.函数值可以为正,也可以为负.形成共价键时要求同号重叠,即对称性匹配原则.

分析两个原子间成键数：成键数=0.5*(成键轨道电子数-反键轨道电子数)

2px和2py形成pi轨道，它们只是坐标不同，形成的成键和反键轨道能量相同，称为简并轨道。

O2中π2px*和π2py*上各有一个电子，称为二价自由基，凡是有未成对电子都称为自由基，要考虑其磁性。

价电子成键理论

两个未配对电子导致的成键

杂化理论

s和p轨道杂化产生的spx轨道能量高于s轨道，低于p轨道，方便成键和形成单电子。杂化所需要的能量由成键时释放的能量提供。

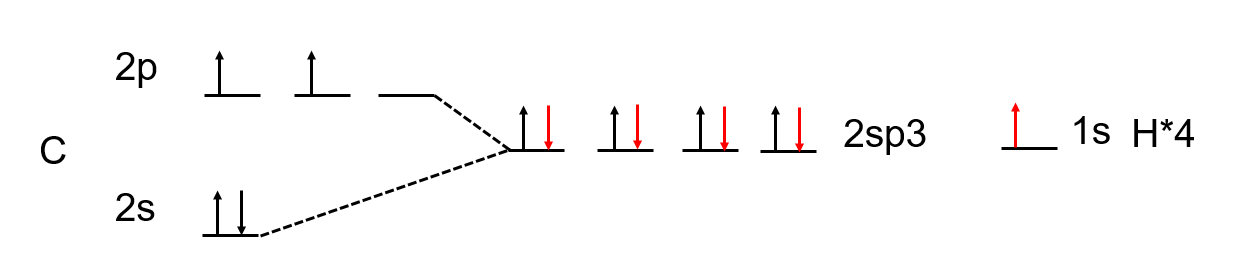
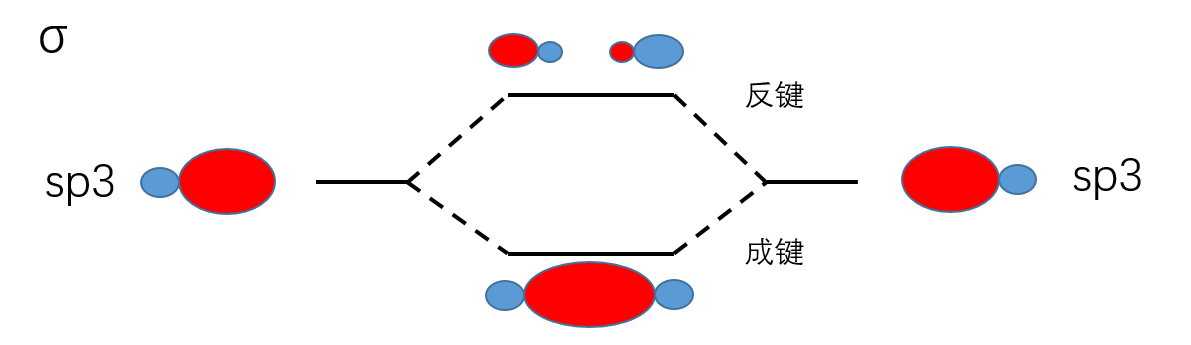
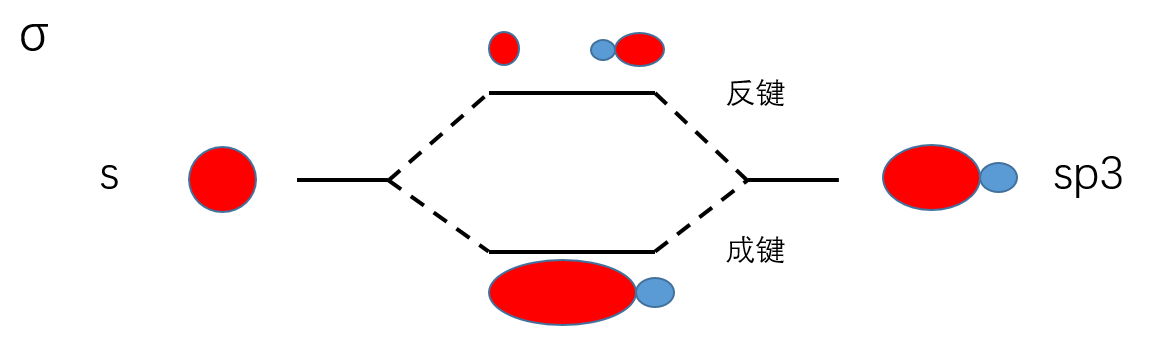
sp3杂化中小的一端是反键，大的一端是成键。

轨道形状

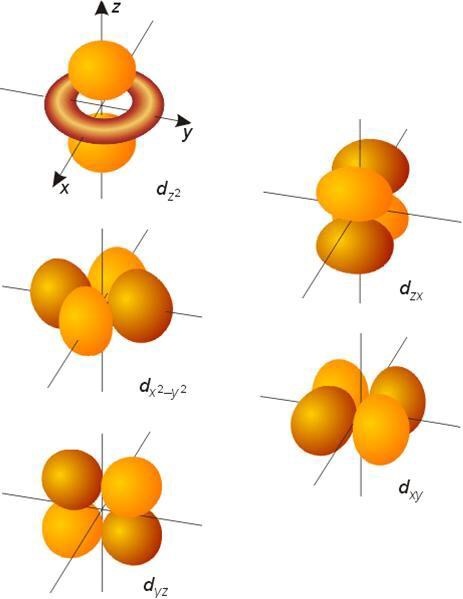
d轨道

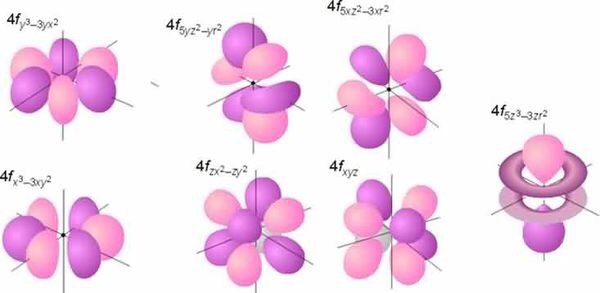
f轨道

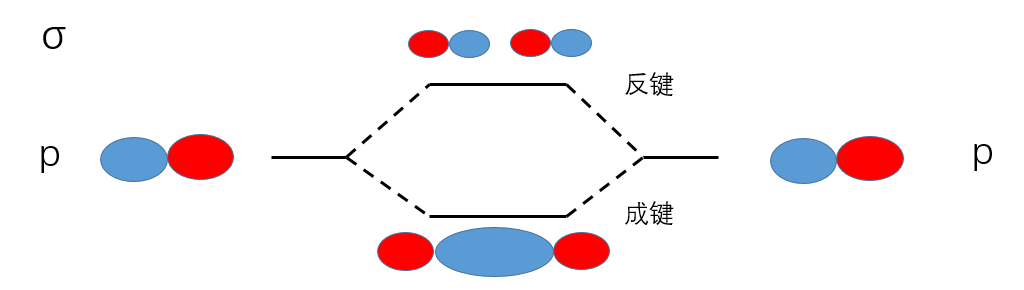
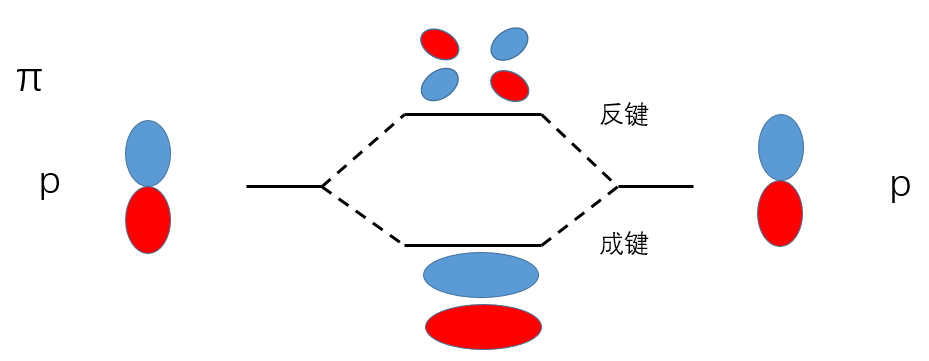
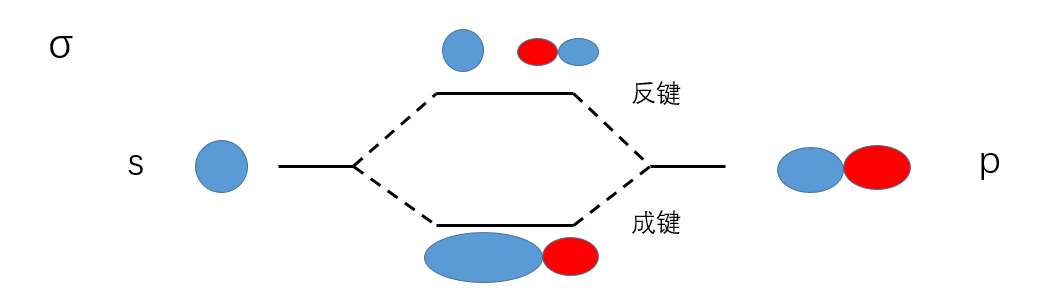
轨道成键形状

下面列举各种相同或不同轨道成键例子

周期性体系

周期性体系分子轨道就变成了能带的概念。能带计算首先计算单点能，保留CHGCAR。

吸附具体过程

但如果只是局部的金属的模型仍然可以用金属原子轨道来讨论

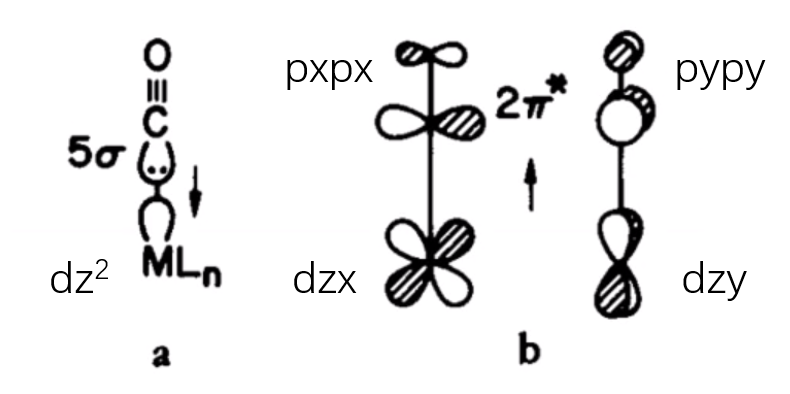
距离CO和Ni表面的成键方式,CO的σ轨道与Ni的dz2轨道头碰头结合，CO的2π*反键轨道与Ni的dzx,dzy以肩并肩方式成键。

活化：活化为吸附后，金属原子的d轨道电子反馈给吸附分子2π*反键轨道电子，因此吸附分子本身的键(如CO中C与O的键)变弱，键长变长。具体表现在DOS图中2π*反键轨道在成键后部分下移到费米能级之下，得到部分电子。因此反键轨道部分移到费米能级下面是活化的证据。

通过DOS可以看出活化过程，而配合ssNBO和COHP可以进一步分析键的成键和键强的变化。

而电荷差分和自旋密度可以分析电子的分布状况。

DOS计算模型准备

切好晶面后添加真空层，固定金属下面几层以准备表面优化，把吸附分子放在真空层(15A)中间，避免吸附分子吸附在上表面或者下表面。这样可以对齐吸附分子和表面的费米能级，方便电子结构分析。对比吸附前和吸附后的DOS图

一般表面计算参数都设置(LREAL = Auto)，ISYM=0去掉对称性

DFT计算时吸附分子之间相距10A，相互作用可以忽略不计

DOS中吸附和金属轨道的重叠可以代表成键的贡献

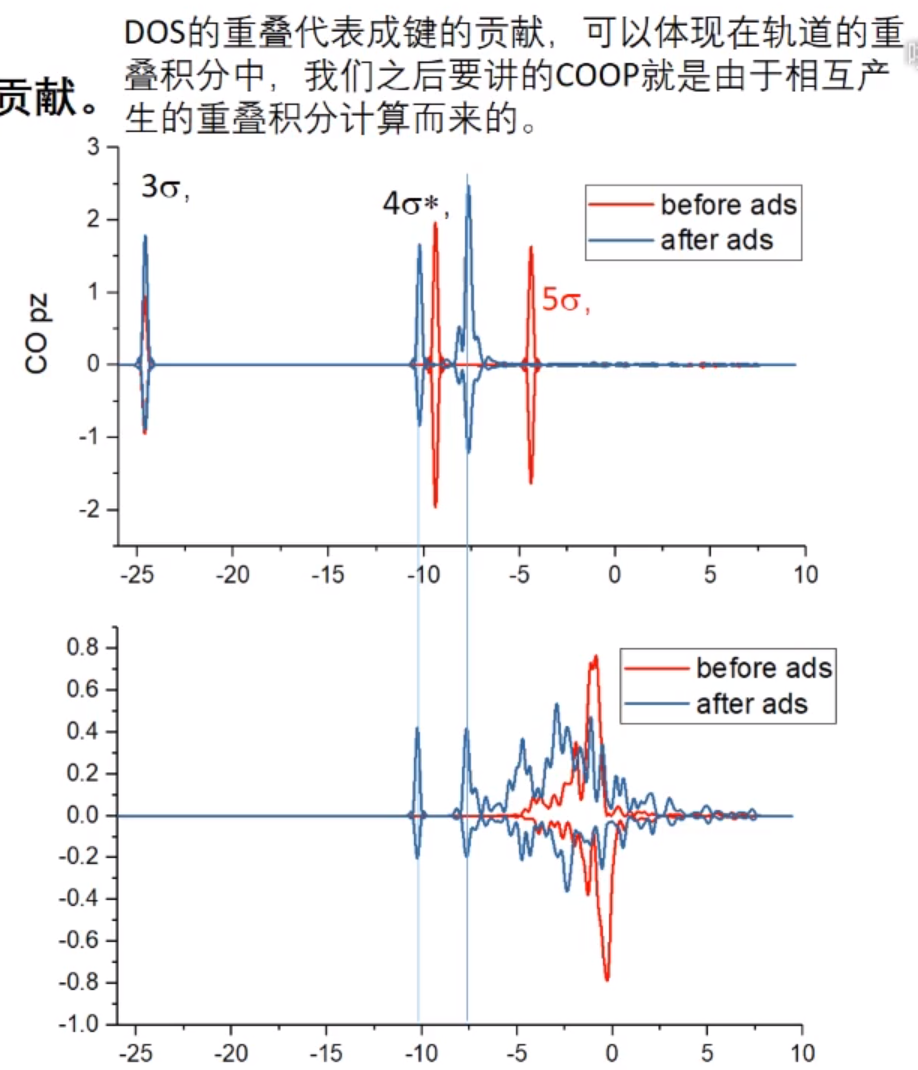
查看不同的轨道对总轨道的贡献，画出单独的吸附质分子的轨道图，分清sigma键和pi键对应的轨道。再画出DOS图，查看是s、px、py、pz哪个轨道给sigma或pi轨道作贡献。

单个吸附分子的DOS和轨道图计算

首先单独优化吸附分子，需要输出WAVECAR

然后查看EIGENVAL文件(cat EIGENVAL)，明确电子占据情况

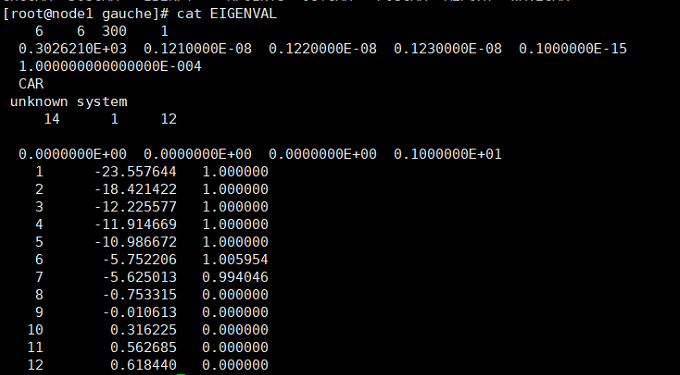
最左边是能带的编号(NBAND)，第二列是能带的能量(eV)，第三列是电子占据数

可以使用vaspkit511的功能来画出轨道图

脚本

for i in $(seq 1 7)

do echo $(i)

echo -e "51\n511\n1\n${i}\n" | vaspkit

done

分子轨道形成与DOS图关系

轨道形成三原则：对称性一致，能量相近，轨道最大重叠。可以根据这三个原则对DOS图分析吸附的具体作用情况。

对称性一致：体现在DOS图中吸附分子是sigma轨道吸附后发生明显变化还是pi轨道发生明显变化；

能量相近：体现在吸附分子与吸附基底能级的位置

轨道重叠：体现在形变后吸附分子和吸附基底的能级轨道是不是位置贴近。

化学键的进一步研究：COOP，COHP

COOP

就是DOS图乘以重叠布局权重，重叠布局只可以在两个原子之间，因此COOP也只可以在两个原子之间。

重叠布局：分子轨道波函数为原子轨道的线性组合：

Φ=c1χ1+c2χ2…\Phi=c_{1} \chi_{1}+c_{2} \chi_{2} \dots

电子分布的概率是归一化的：

1=∫∣Φ2∣dτ=∫∣c1χ1+c2χ2∣2dτ=c12+c22+2c1c2S121=\int\left|\Phi^{2}\right| d \tau=\int\left|c_{1} \chi_{1}+c_{2} \chi_{2}\right|^{2} d \tau=c_{1}^{2}+c_{2}^{2}+2 c_{1} c_{2} S_{12}

其从S12S_{12}是两个原子波函数之间的重叠积分。2c1c2S122c_1c_2S_{12}是相互作用有关的量，称为重叠布局。如果c1c2c_1c_2同号，则为正值(成键)，如果c1c2c_1c_2反号，则为负值(反键)。

因此乘以重叠布局权重后可以判断成键和反键，重叠程度大小情况。COOP费米能级以下的积分值可以反应键强。对比吸附前后的COOP可以分析键强的变化。

d带中心

配位数增加可以使d带更宽，d带中心下降，降低吸附能。

当晶格中分子之间距离边长，d带宽度变窄，吸附能增加。

DFT分析金属稳定性

可以分析空位形成能来分析稳定性(DOI: 10.1021/jacs.8b08836)